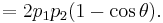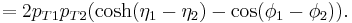Invariant mass
The invariant mass, rest mass, intrinsic mass, proper mass or just mass is a characteristic of the total energy and momentum of an object or a system of objects that is the same in all frames of reference related by Lorentz transformations. When the system as a whole is at rest (or when it equivalently has zero net momentum), the invariant mass is equal to the total energy of the system divided by c2. See mass-energy equivalence for a discussion of definitions of mass. Since the mass of systems must be measured with a weight or mass scale in a reference frame in which the system has zero momentum (the center of momentum frame), such a scale always measures the system's invariant mass.
Systems whose four-momentum is a null vector have zero invariant mass and are referred to as massless. There are no physical objects which appear to have space-like four-momenta. For an isolated massive system, those four-momentum is a time-like vector, the center of mass moves in a straight line with a steady sub-luminal velocity, and an observer can always move along with it. In this frame, the center of momentum frame, the total momentum is zero, the system as a whole may be thought of as being "at rest" if it is a bound system (like a bottle of gas), and the invariant mass of the system is equal to the total system energy divided by c2. This total energy in the center of momentum frame, is the minimum energy which the system may be observed to have, when seen by various observers from various inertial frames.
If the system consists of more than one particle, the particles may be moving relative to each other in the center of momentum frame, and they will generally interact through one or more of the fundamental forces. The kinetic energy of the particles and the potential energy of the force fields increase the total energy above the sum of the particle rest masses, and contribute to the invariant mass of the system. The sum of the particle kinetic energies as calculated by an observer is smallest in the center of momentum frame (or rest frame if the system is bound).
Contents |
Particle physics
In particle physics, the invariant mass is a mathematical combination of a particle's energy E and its momentum p which is equal to the mass in the rest frame. This invariant mass is the same in all frames of reference (see Special Relativity).
or in natural units where c = 1,
This equation says that the invariant mass is the pseudo-Euclidean length of the four-vector (E, p), calculated using the relativistic version of the pythagorean theorem which has a different sign for the space and time dimensions. This length is preserved under any Lorentz boost or rotation in four dimensions, just like the ordinary length of a vector is preserved under rotations. In quantum theory the invariant mass is a parameter in the relativistic Dirac equation for an elementary particle. The Dirac quantum operator corresponds to the particle four-momentum vector.
Since the invariant mass is determined from quantities which are conserved during a decay, the invariant mass calculated using the energy and momentum of the decay products of a single particle is equal to the mass of the particle that decayed. The mass of a system of particles can be calculated from the general formula:
where
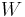 is the invariant mass of the system of particles, equal to the mass of the decay particle.
is the invariant mass of the system of particles, equal to the mass of the decay particle. is the sum of the energies of the particles
is the sum of the energies of the particles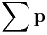 is the vector sum of the momentum of the particles (includes both magnitude and direction of the momenta)
is the vector sum of the momentum of the particles (includes both magnitude and direction of the momenta)
The term invariant mass is also used in inelastic scattering experiments. Given an inelastic reaction with total incoming energy larger than the total detected energy (i.e. not all outgoing particles are detected in the experiment), the invariant mass (also known as the "missing mass") 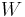 of the reaction is defined as follows:
of the reaction is defined as follows:
If there is one dominant particle which was not detected during an experiment, a plot of the invariant mass will show a sharp peak at the mass of the missing particle.
In those cases when the momentum along one direction cannot be measured (i.e. in the case of a neutrino, whose presence is only inferred from the missing energy) the Transverse mass is used.
Example: two-particle collision
In a two-particle collision (or a two-particle decay) the square of the invariant mass (in natural units) is
Massless particles
The invariant mass of a system made of two massless particles whose momenta form an angle  has a convenient expression:
has a convenient expression:
Collider Experiments
In particle collider experiments, one often defines the angular position of a particle in terms of a azimuthal angle  and pseudorapidity
and pseudorapidity 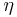 . Additionally the transverse momentum,
. Additionally the transverse momentum, 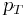 , is usually measured. In this case if the particles are massless, or highly relativistic (
, is usually measured. In this case if the particles are massless, or highly relativistic ( 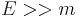 ,) then the invariant mass becomes:
,) then the invariant mass becomes:
Rest energy
The rest energy 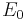 or rest energy of a particle is defined as:
or rest energy of a particle is defined as:
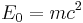 ,
,
where  is the speed of light in a vacuum.[1] In general, only differences in energy have physical significance.[2]
is the speed of light in a vacuum.[1] In general, only differences in energy have physical significance.[2]
The concept of rest energy follows from the Special theory of relativity that leads to Einstein's famous conclusion about equivalence of energy and mass. See background for mass-energy equivalence.
On the other hand, the concept of the equivalent Dirac invariant rest mass may be defined in terms of the self energy corresponding to the product of a geometric matter current and a generalized potential [3] as part of a single definition of mass in a geometric unified theory.
See also
References
- Landau, L.D., Lifshitz, E.M. (1975). The Classical Theory of Fields: 4-th revised English Edition: Course of Theoretical Physics Vol. 2. Butterworth Heinemann. ISBN 0-7506-2768-9.
- Okun, L.B. (1989). The Concept of Mass. http://www.worldscibooks.com/etextbook/6833/6833_02.pdf.
- Halzen, Francis; Martin, Alan (1984). Quarks & Leptons: An Introductory Course in Modern Particle Physics. John Wiley & Sons. ISBN 0-471-88741-2.
Citations
- ^ http://www.prod.sandia.gov/cgi-bin/techlib/access-control.pl/2006/066063.pdf
- ^ Modell, Michael; Robert C. Reid (1974). Thermodynamics and Its Applications. Englewood Cliffs, NJ: Prentice-Hall. ISBN 0-13-914861-2.
- ^ González-Martín, Gustavo R. (1994). "A geometric definition of mass.". Gen. Rel. and Grav. 26: 1177. Bibcode 1994GReGr..26.1177G. doi:10.1007/BF02106710. http://www.springerlink.com/content/k7436p075454jtg5/.
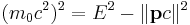
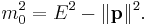
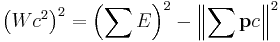
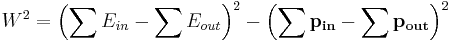
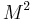
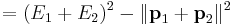
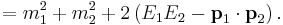
![= [(p_1,0,0,p_1)%2B(p_2,0,p_2\sin\theta, p_2\cos\theta)]^2 = (p_1%2Bp_2)^2 -p_2^2\sin^2\theta -(p_1 %2B p_2\cos\theta)^2 \,](/2012-wikipedia_en_all_nopic_01_2012/I/523e94b14e533604a2896bbed66836a4.png)